Übung Boxplot

Überblick Lektion 1

Boxplot:
Beispiel mit RÜben

Für den Boxplot ist es sinnvoll, eine etwas größere Datenmenge zu verwenden. Wir benutzen einen Zufallsgenerator, um eine Datenreihe mit 1000 Werten zu erzeugen:

x <- round(10*rnorm(1000))+50

Mit einem Histogramm kann man sich die Verteilung der Werte ganz gut veranschaulichen:

hist(x)

Quartile und Boxplot anzeigen: ℹ️ Hinweis

quantile(x)
boxplot(x, horizontal=T)

Wir machen den Boxplot horizontal, damit wir ihn leichter mit dem Histogramm und den Quartilen vergleichen können.

     0%   25%   50%   75%   100%
     19    43    50    57    80

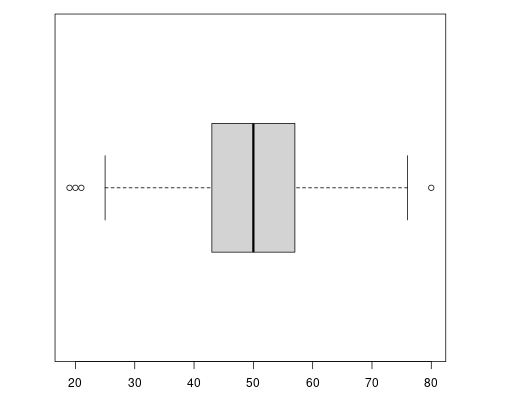
Der Streubereich ist der Bereich vom kleinsten bis zum größten Wert:

range(x)
[1]  19  80

Die Spannweite ist die Differenz davon:

diff( range(x) )
[1]  61

Der Interquartilsbereich ist der Bereich von Q1 bis Q3:

Q1 <- quantile(x, 0.25)
Q3 <- quantile(x, 0.75)
c(Q1, Q3)
25%   75%
 43    57

Im Boxplot ist das genau der Bereich der Box.

Der Interquartilsabstand ist die Differenz davon:

IQR(x)
[1]  14
 
x <- round(10*rnorm(1000))+50
hist(x)
quantile(x)
boxplot(x, horizontal=T)
range(x)
diff(range(x))
Q1 <- quantile(x, 0.25)
Q3 <- quantile(x, 0.75)
c(Q1, Q3)
IQR(x)
Hinweis

Das Fenster mit dem  grünen Button  ist eine R Konsole. Es verhält sich im Prinzip genauso, wie die R Konsole in deinem RStudio. Du kannst damit "rumspielen", die Zahlen verändern und Dinge ausprobieren.

Du kannst nichts kaputt machen! Den Ausgangszustand kannst du jederzeit durch einen Seiten Reload wiederherstellen.


  ⬜ gesehen    ⬜ verstanden  
 (Markierung auch in der Lektion Übersicht)

4 Gedanken zu „Übung Boxplot“

    1. Es ist ein spezialisiertes Grafikpaket, das deutlich mehr Möglichkeiten hat als das R Basispaket, wenn es z.B. um die Darstellung von sehr ausgefeilten Diagrammen geht.

      Ich finde es für einen Statistik Grundkurs eigentlich überflüssig und deplatziert. Aber in den Moodle-Tutorials des M2 Moduls wird es für Grafiken (leider) ausschließlich genutzt…

Schreibe einen Kommentar