ℹ️ Hinweis ← (hier klicken)
Aufgabe 1
Der Korrelationskoeffizient für den Zusammenhang zwischen der Postleitzahl und der Körpergröße ist im Text angegeben mit r = 0,02.
Es wurde nicht einfach nur die Korrelation berechnet, sondern es wurde ein t-Test für die Korrelation gemacht:
Hier ist ein Beispiel, um die Aufgabe zu veranschaulichen:
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Lösungen:
- 💡 A ist falsch: Wie der Effekt in der Population ist, wissen wir nicht genau. Aber da der Effekt in der sehr großen Stichprobe (n=40.000) klein ist, kann man ziemlich sicher davon ausgehen, dass der Effekt in der Population nicht sehr groß ist. Aufgrund der sehr großen Stichprobe werden auch kleine Effekte signifikant.
- 💡 B ist richtig: Siehe oben. Große Stichproben werden bereits bei kleinen Effekten signifikant. ℹ️ Demo.
- 💡 C ist falsch: 1% ist nicht unüblich hoch.
- 💡 D ist richtig: Diese Aussage wurde vom Lehrstuhl offenbar als falsch gewertet, aber mir ist absolut schleierhaft warum. Da der Lehrstuhl seine Bewertungen grundsätzlich nicht erläutert oder begründet, kann man darüber nur spekulieren. Aber tatsächlich ist diese Aussage eindeutig richtig. Wenn man
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.Signifikanz heißt nicht, dass der Effekt in der Stichprobe groß ist, sondern dass er vorhanden und statistisch relevant ist. - 💡 E ist falsch: Die PLZ ist zwar eigentlich keine metrische Größe, sondern eine ID-Nummer, um eine Stadt (oder Bezirk) zu identifizieren. Dennoch kann man mit R die Korrelation zwischen PLZ und Körpergröße berechnen. Und zwar auch dann, wenn die ℹ️ PLZ gar nicht als numerischer Wert, sondern als Textvariable vorliegt. Ob der PMK in diesem Fall auch irgend einen Sinn ergibt, ist für R egal. Mit R kann man alles berechnen. Diese Aussage ist also in jedem Fall falsch.
Aufgabe 2
pwr::pwr.r.test(r=0.25, power=0.80, alternative="greater")
approximate correlation power calculation (arctangh transformation)
n = 96.77644
r = 0.25
sig.level = 0.05
power = 0.8
alternative = greater
frameborder='0'>
Lösungen:
- 💡 A ist falsch: Siehe Output,
sig.level = 0.05. Das ist die Standardeinstellung, wenn man den Parametersig.levelbeim Aufruf der Funktion einfach weglässt. - 💡 B ist falsch: Der angenommene Effekt ist
r = 0.25. - 💡 C ist falsch: Es handelt sich um eine Poweranalyse für einen t-Test für Korrelation:
correlation power calculation - 💡 D ist falsch:
alternative = greater. - 💡 E ist falsch: Die Power ist:
power = 0.8, also 80%. Bei der 96.77644 handelt es sich um die (vermutlich empfohlene) Stichprobengröße:n = 96.77644
Aufgabe 3
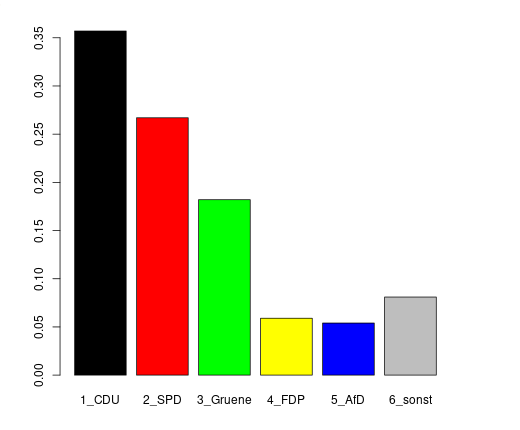
Es ist das Ergebnis einer Landtagswahl als Säulendiagramm dargestellt.
Wenn man die Prozente einfach mal auf "pro Tausend" hochrechnet, kann man die dargestellte Stimmenverteilung wie folgt erzeugen:
stimmen <- c(rep("1_CDU", 357), rep("2_SPD", 267), rep("3_Gruene", 182), rep("4_FDP", 59), rep("5_AfD", 54), rep("6_sonst", 81))
Häufigkeitstabelle für die relativen Häufigkeiten:
prop.table( table(stimmen) )
stimmen
1_CDU 2_SPD 3_Gruene 4_FDP 5_AfD 6_sonst
0.357 0.267 0.182 0.059 0.054 0.081
Diese Häufigkeiten können jetzt mithilfe der barplot()-Funktion in einem Säulendiagramm dargestellt werden.
Vorher definieren wir noch die Farben:
colors = c("black", "red", "green", "yellow", "blue", "gray")
Säulendiagramm für die relativen Häufigkeiten:
barplot( prop.table(table(stimmen)), col=colors)
Lösungen:
- 💡 A ist falsch: Es gibt keinen Chi-Quadrat-Test für eine Stichprobe, sondern nur für eine Variable. Darum ist die Aussage als falsch zu bewerten. Tatsächlich wäre der Chi-Quadrat-Test für eine Variable geeignet, um zu prüfen, ob die Verteilung in der Stichprobe ℹ️ signifikant von einer Gleichverteilung abweicht.
- 💡 B ist richtig
- 💡 C ist richtig: Man kann die jeweils gewählte Partei in R auch ℹ️ als Faktor-Datentyp ablegen.
- 💡 D ist richtig
- 💡 E ist falsch: Bei einer Varianzanalyse werden die Mittelwerte von mehreren Gruppen verglichen. Was sollten hier die Gruppen sein? Es gibt keine Gruppen und keine Gruppierungsvariable. Es gibt keine UV und keine AV. Wir sehen die ℹ️ Häufigkeiten der verschiedenen Ausprägungen einer einzigen nominalen Variable.
Aufgabe 4
Dargestellt ist der Output einer Varianzanalyse.
Mit der Varianzanalyse kann man prüfen, ob sich die Mittelwerte von mehr als zwei Gruppen signifikant unterscheiden.
Hier ist ein ähnliches Beispiel, um die Aufgabe zu veranschaulichen:
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Lösungen:
- 💡 A ist falsch: Es sind drei Freiheitsgrade, also wurden vier Länder miteinander verglichen. Siehe oben.
- 💡 B ist richtig: Siehe oben.
- 💡 C ist falsch: Der Datensatz ist
plf. - 💡 D ist richtig: Der dargestellte p-Wert ist kleiner als
0,05. - 💡 E ist richtig: Die Spalte ℹ️ Mean Sq enthält die Varianzen.
Aufgabe 5
Lösungen:
- 💡 A ist falsch: Richtig wäre t-Test für abhängige Stichproben. Es geht um Wertepaare: Die Anzahl der Migräne-Tage vorher und nachher.
- 💡 B ist falsch: Korrelation ist nicht Kausalität!! Über die Ursache ist nichts bekannt! ☝️ Merke: Wann immer in einer Aussage von einer Ursache (einem Grund) oder einem Kausalzusammenhang die Rede ist, ist die Aussage vermutlich als falsch zu bewerten.
- 💡 C ist richtig: Die Ärztin "hat die Hypothese, dass ihre Behandlung ... zu weniger Migräne-Tagen" führt.
- 💡 D ist falsch: Cramers Phi ein Zusammenhangsmaß für nominale Merkmale. Siehe Lektion 3 - Nominale Zusammenhangsmaße. Aber die Anzahl der Migräne-Tage ist eine metrische Größe.
- 💡 E ist richtig: ℹ️ Beispiel.
Aufgabe 6
Diese Aufgabe ist ähnlich wie:
- Aufgabe 14 aus der Klausur 03/2022
- Aufgabe 4 aus der Klausur 09/2021 und
- Aufgabe 5 aus der Klausur 03/2021.
Es geht um die Frage, ob und wie die Zufriedenheit im Job von der Anzahl der Dienstjahre abhängt. Dieser Zusammenhang ist für drei verschiedene Geschlechtergruppen (m/w/d) in unterschiedlichen Farben dargestellt.
Beim dargestellten Diagramm handelt es sich also im Grunde um drei Streudiagramme, die in einem Bild dargestellt werden. Für jedes Streudiagramm eine andere Farbe.
Das nennt man auch gruppiertes Streudiagramm: Jede Gruppe hat eine andere Farbe, also hat quasi jede Gruppe ein eigenes Streudiagramm.
Hier ist ein ähnliches Beispiel um die Aufgabe zu veranschaulichen:
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Lösungen:
- 💡 A ist falsch: Der Regressionskoeffizient b ist die Steigung der Gerade. Die ist (in der Aufgabe) bei den männlichen Angestellten flacher, also kleiner.
- 💡 B ist falsch: Der Koeffizient a ist der Schnittpunkt mit der Y-Achse. Der ist bei der grünen Linie (in der Aufgabe) ungefähr bei 2,3 (die Y-Achse müsste man da einzeichnen, wo X=0 ist).
- 💡 C ist falsch: Es ist ein Streudiagramm (oder Scatterplot). Bei einem Histogramm handelt es sich um die Häufigkeitsverteilung einer einzigen Variable. Hier geht es um den Zusammenhang von zwei Variablen.
- 💡 D ist richtig: Da es nur bei den ℹ️ wenigen Diversen eine fallende Gerade gibt, kann man per Augenmaß durchaus sagen, dass es für alles zusammen einen positiven Zusammenhang gibt.
- 💡 E ist falsch: Mit anderen Worten lautet die Frage, ob die Steigung der Gerade, also der Koeffizient b für die Männer gleich eins ist (wenn die Anzahl der Jahre um eins zunimmt, dann nimmt auch der Zufriedenheitswert um eins zu). Im dargestellten Diagramm würde das bedeuten: Ein Kästchen nach rechts - zwei Kästchen nach oben (jeweils eine Maßeinheit). Das ist bei der roten Gerade für die Männer nicht der Fall.
Aufgabe 7
Lösungen:
- 💡 A ist richtig: Bootstrapping funktioniert auch, wenn die Daten nicht normalverteilt sind. Das gilt als einer der beiden ℹ️ Vorteile des Resampling.
- 💡 B ist richtig: Das ist der andere ℹ️ Vorteil des Resampling.
- 💡 C ist richtig: Es ist wirklich verrückt, dass diese Aufgabe praktisch identisch aus dem letzten Semester übernommen wurde, obwohl sie
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben. - 💡 D ist richtig: Je größer die Stichprobe, desto kleiner der Standardfehler und desto schmaler das KI.
- 💡 E ist richtig: Es gibt auch einseitige Konfidenzintervalle, die auf einer Seite bis unendlich gehen.

Hallo Guido. Hier sind Lösungen mit deine Kommentare, was absolute Vorteil ist. Aber wo findet man eigentlich die original Fragen zu diese Aufgaben?
Lg
Die Fragen sind hier:
https://psycho-hagen.statstutor.de/statstutor/m2-statistik/klausurvorbereitung/uebungsaufgaben/