ℹ️ Hinweis ← (hier klicken)
Aufgabe 1
Bei dieser Aufgabe ist ein Balkendiagramm dargestellt. Offenbar ist es dem Lehrstuhl wichtig, diesen Unterschied zwischen Säulen- und Balkendiagramm zu machen. Demnach ist ein Balkendiagramm ein um 90 Grad gedrehtes Säulendiagramm. Diese ℹ️ etwas eigenwillige Definition stammt aus dem Eid S.131/132. Siehe dazu auch Aufgabe 2D aus 03/2021.
Lösungen:
- 💡 A ist falsch Siehe oben.
- 💡 B ist falsch Es sind nicht 30.000 Personen, sondern 30 Prozent der Befragten.
- 💡 C ist falsch "1000-3600 Befragte je Land"
- 💡 D ist richtig Das Land ist ein nominales Merkmal.
- 💡 E ist falsch Nicht die Größe der Population beeinflusst die Breite des KI, sondern die Größe der Stichprobe.
Aufgabe 2
Bei dieser Aufgabe geht es um die korrekte Einordnung der Begriffe Prozentrang, Quantil und Z-Wert.
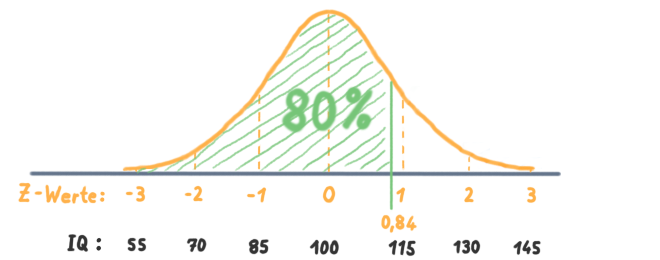
Wenn man einfach mal davon ausgeht, dass der mittlere IQ gleich 100 ist, und die Standardabweichung ist 15, dann ergibt sich das folgende Bild:
Lösungen:
- 💡 A ist falsch: Umgekehrt. 80% haben einen niedrigeren IQ.
- 💡 B ist richtig: Der Prozentrang ist praktisch dasselbe wie die kumulierte relative Häufigkeit. Und das 0,8-Quantil ist ja an der Stelle, wo die kumulierte relative Häufigkeit 0,8 ist.
- 💡 C ist richtig: Der Durchschnitt ist in der Mitte beim 0,5-Quantil, denn "die IQ-Werte sind normalverteilt".
- 💡 D ist falsch: Das 0,8-Quantil der Standardnormalverteilung ist 0,84.
Z0,8 = 0,84. Siehe Sedlmeier S.1040 oder Wikipedia (alternativ kann man in seinem RStudio auch einfach malqnorm(0.8)eintippen). In der Klausur wurden jedoch beide Antwortmöglichkeiten als richtig gewertet. Ich bin mir nicht ganz sicher warum. Entweder weil 0,84 so nah an 0,8 ist (so die Argumentation im ↗️ Feedbackbrief) oder weil das Nachschlagen eines Z-Quantils in der Tabelle als nicht klausurrelevant erachtet wurde (obwohl es eine OpenBook Klausur war). - 💡 E ist richtig: Der Prozentrang bezieht sich, wie das Quantil, auf die sortierten Daten.
Aufgabe 3
Welche Aussagen zur linearen Regression sind richtig?
Lösungen:
- 💡 A ist richtig: X ist der Prädiktor und Y ist das Kriterium.
- 💡 B ist richtig: Der Determinationskoeffizient r2 ist die Regressionsvarianz geteilt durch die Gesamtvarianz von Y, ergibt also den Anteil. Siehe auch Zusammenfassung Varianzzerlegung.

- 💡 C ist richtig: Die Regressionsgerade ist die Gerade mit den geringsten quadrierten Y-Abweichungen. Siehe Lernkarten Varianzzerlegung (Karte 14).
- 💡 D ist falsch Der Determinationskoeffizient ist gleich dem Korrelationskoeffizient zum Quadrat. Siehe Zusammenfassung Varianzzerlegung (ganz unten).
- 💡 E ist richtig:
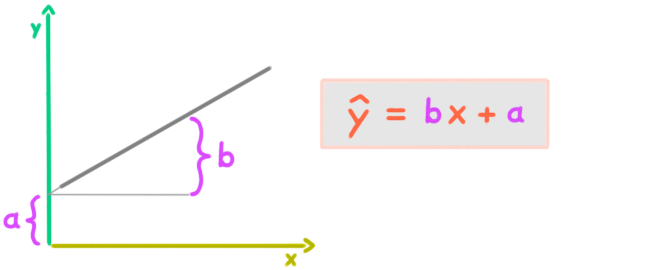
1,5 ist die Steigung der Regressionsgerade. Das ist der Regressionskoeffizient b (das sogenannte Regressionsgewicht). Siehe Zusammenfassung Regression.
Aufgabe 4
Lösungen:
- 💡 A ist richtig: Das ist die allgemeine Formulierung des Zentralen Grenzwertsatzes. Siehe Sedlmeier S.337. Für Details zum ZGS siehe Lektion 6.
- 💡 B ist richtig: Xquer ist der Schätzwert für Mü.
- 💡 C ist richtig
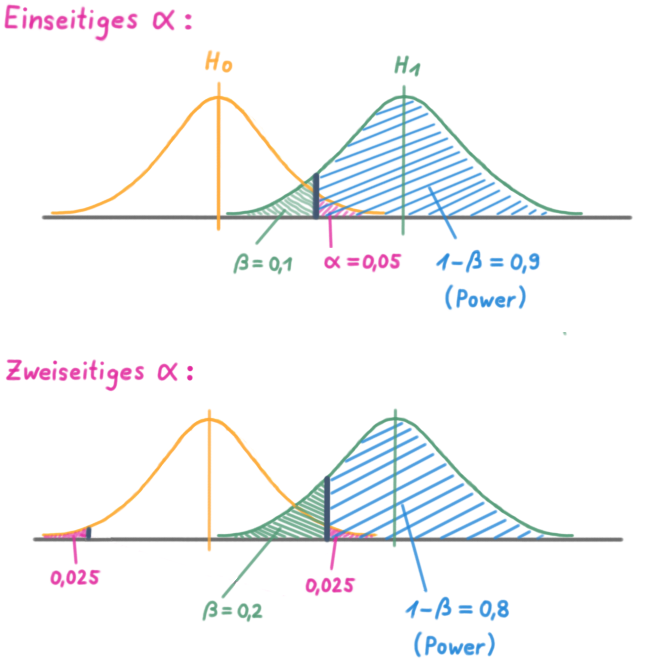
- 💡 D ist falsch: Großes Alpha (α) –> große Power:

- 💡 E ist richtig: Das ist im Prinzip dieselbe Aufgabe wie bei Aussage 6A aus 03/2021. Einseitige Tests haben (im Vergleich zu zweiseitigen) die größere Power. Beispiel: Beide unten dargestellten Tests haben ein Signifikanzniveau von 5 Prozent. Aber der einseitige Test hat die größere Power (im Beispiel 0,9 vs. 0,8), weil sich das Signifikanzniveau Alpha (α) beim zweiseitigen Test auf beide Seiten aufteilt:
Aufgabe 5
Lösungen:
- 💡 A ist richtig: Einer der beiden ℹ️ Vorteile des Resampling ist, dass es für beliebige Kennzahlen funktioniert. Auch wenn dieses Beispiel reichlich sinnlos erscheint und überhaupt nicht plausibel, warum das jemand wollen würde, so kann man auch ein KI für die Differenz von Standardabw. und MW berechnen.
- 💡 B ist falsch: Beim Bootstrap wird normalerweise immer mit Zurücklegen gezogen. Bei anderen Resampling-Verfahren ist beides möglich, sowohl mit als auch ohne Zurücklegen. Siehe Sedlmeier S.609.
- 💡 C ist falsch: Selbstverständlich müssen die Stichproben auch bei Resampling-Verfahren möglichst repräsentativ sein.
- 💡 D ist falsch: Resampling-Verfahren sind immer eine gangbare Alternative zu den "konventionellen" Testverfahren.
- 💡 E ist falsch: Die Resampling-Stichprobe kann auch genauso groß sein, wie die ursprüngliche Stichprobe. Sie muss deswegen nicht identisch sein, weil man ja auch mit Zurücklegen ziehen kann. Siehe z.B. Sedlmeier S.592.
Aufgabe 6
Dargestellt ist der Output einer Varianzanalyse.
Mit der Varianzanalyse kann man prüfen, ob sich die Mittelwerte von mehr als zwei Gruppen signifikant unterscheiden.
Hier ist ein ähnliches Beispiel, um die Aufgabe zu veranschaulichen:
Daten für vier Kitas per Zufallsgenerator erstellen:
kita1 <- sample(1:5, 14, replace=TRUE)
kita2 <- sample(1:5, 14, replace=TRUE)
kita3 <- sample(1:5, 14, replace=TRUE)
kita4 <- sample(1:5, 15, replace=TRUE)
Und in einem Data Frame zusammenführen:
kf1 <- data.frame(zufr=kita1, kita="kita1")
kf2 <- data.frame(zufr=kita2, kita="kita2")
kf3 <- data.frame(zufr=kita3, kita="kita3")
kf4 <- data.frame(zufr=kita4, kita="kita4")
kita <- rbind(kf1, kf2, kf3, kf4)
#kita
(um dir die Daten anzuschauen, musst du einfach nur das Kommentarzeichen (#) in der letzten Zeile entfernen)
Mit diesen Daten können wir die Anova rechnen:
summary(aov(kita$zufr ~ kita$kita))
(da die Daten per Zufallsgenerator erzeugt werden, ist das Ergebnis jedes Mal ein bisschen anders)
Df Sum Sq Mean Sq F value Pr(>F)
kita$kita 3 5.01 1.670 1.03 0.387
Residuals 53 85.97 1.622
Lösungen:
- 💡 A ist falsch: Die Anzahl der Zählerfreiheitsgrade ist 3. Aber die Anzahl der Zählerfreiheitsgrade ist gleich der Anzahl der Gruppen minus eins. Also wurden die Eltern von vier Kitas befragt. Siehe auch das Beispiel oben.
- 💡 B ist falsch: Der p-Wert in der Aufgabe ist 0,975, also fast 1. Das heißt, die Gruppen unterscheiden sich im Durchschnitt so gut wie gar nicht.
- 💡 C ist richtig: Es gibt nur einen Faktor, nach dem die Gruppen unterschieden werden: Die Kita-Zugehörigkeit.
- 💡 D ist richtig: Bei der Varianzanalyse werden alle Gruppen gleichzeitig auf (Un-)Gleichheit getestet. Es werden nicht einzelne Gruppen miteinander verglichen, sondern es ist ein Gesamt-Test über alles (over all). Es ist ein Overall-Test. Dementsprechend bezeichnet man die Alternativhypothese manchmal auch als ℹ️ Overall-Hypothese. Sie sagt nicht, dass sich bestimmte Mittelwerte unterscheiden, sondern sie sagt nur, die Mittelwerte unterscheiden sich irgendwie. Sie bezieht sich also auf alle Mittelwerte gleichzeitig. Daher wird sie manchmal auch als Omnibus-Hypothese bezeichnet (omnibus ist latein für alle). Diese Frage ist praktisch identisch zu Aussage 7A in der Klausur 09/2021.
- 💡 E ist falsch: Der Datensatz heißt
KiTa. Und die Variable für die Gruppenzugehörigkeit heißt ebenfallsKiTa.Dfsind die Freiheitsgrade (Degrees of Freedom).

Aufgabe 7
Es wird die Konzentrationsfähigkeit von drei Gruppen (in drei verschiedenen Räumen) verglichen.
Hier ist ein Beispiel mit Grafik, um die Aufgabe anschaulicher zu machen:
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Lösungen:
- 💡 A ist richtig: Mit der Varianzanalyse kann man die Mittelwerte von mehr als zwei Gruppen vergleichen.
- 💡 B ist falsch: Der U-Test ist die Alternative für den t-Test für zwei unabhängige Stichproben. Als Alternative für die Varianzanalyse für mehr als zwei Stichproben ist der Kruskal-Wallis-Test die richtige Alternative. Siehe Zusammenfassung non-parametrische Tests.
- 💡 C ist falsch: Richtig wäre der t-Test für unabhängige Stichproben. "Die Proband:innen werden per Zufall verschiedenen Räumen zugeordnet". Bei abhängigen Stichproben müsste man irgendwie Wertepaare bilden können.
- 💡 D ist falsch: Die Varianzanalyse funktioniert auch prima ℹ️ mit unterschiedlich großen Stichproben.
- 💡 E ist falsch: Der Sinn dieser Aussage erschließt sich mir nicht. Vielleicht sollen die Studis einfach nur mit möglichst verwirrenden Aussagen verunsichert werden... Anhand der vorliegenden Informationen kann man die Aussage jedenfalls nicht bewerten. Vielleicht ging es dem Lehrstuhl einfach nur darum, dass man anhand der Abweichung der Punktezahlen nicht auf die Signifikanz schließen kann. Die Signifikanz ergibt sich einzig aus dem p-Wert. Der ist hier nicht angegeben und er lässt sich auch nicht herleiten.
Aufgabe 8
Bei dieser Aufgabe geht es um den Zusammenhang zwischen zwei nominalen Merkmalen: dem Raucherstatus (in den Tabellenzeilen) und der Zugehörigkeit zu einer von mehreren Peer-Gruppen (die Spaltenüberschriften).
Den Zusammenhang zwischen zwei nominalen Merkmalen überprüft man mit dem Chi-Quadrat-Test für zwei Variablen.
Bei der Tabelle handelt es sich also um eine Art Kreuztabelle / Kontingenztafel. Angegeben sind jeweils die absoluten Häufigkeiten und daneben auch noch die Prozentangaben pro Spalte ("Total n" ist jeweils die Summe der Spalte und "Total %" ist jeweils 100 Prozent).
Um die einzelnen Aussagen auf Richtigkeit zu überprüfen, müssen ein paar Informationen aus dem Text und der dargestellten Tabelle abgelesen werden.
Lösungen:
- 💡 A ist richtig: "The relationship was significant X2(8, n=5153) = 387.35, p<0.001". Der p-Wert ist also kleiner als 0,001. Das heißt: bei einem Niveau von 5% deutlich signifikant.
- 💡 B ist falsch:
"Total n"ist in allen Gruppen unterschiedlich. - 💡 C ist falsch: Es war ein Chi-Quadrat-Test für zwei Variablen. Es geht um den Zusammenhang von zwei Variablen: dem Raucherstatus und der Gruppenzugehörigkeit.
- 💡 D ist richtig: Der Prozentwert von 25.64 ist größer als die Prozentwerte der anderen Gruppen in dieser Zeile.
- 💡 E ist falsch: Andersrum: 11,25% der "Mainstream peer crowd" sind "Experimenter". Die Prozentzahlen innerhalb einer Gruppe addieren sich immer zu 100%.
Aufgabe 9
Der Korrelationskoeffizient für den Zusammenhang von Tagestemperatur und Benzinpreis ist im Text angegeben mit r = -0,45.
Die Korrelation ist also negativ. Das bedeutet: Je niedriger die Temperatur, desto größer der Benzinpreis.
Es wurde nicht einfach nur der Korrelationskoeffizient ausgerechnet, sondern es wurde ein t-Test für die Korrelation gemacht:
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Lösungen:
- 💡 A ist richtig: Es gilt grundsätzlich immer: Je größer n, desto größer die Power. Also wird ein derart starker Zusammenhang (r=-0,45) bei einem ausreichend großen n sicher signifikant werden. ℹ️ Siehe hier zum Beweis.
- 💡 B ist falsch: Der Korrelationskoeffizient r gilt hier auch als Effektgröße. Ein Korrelationskoeffizient von -0.45 gilt gemäß Cohen als eher starker Zusammenhang, also als großer Effekt. Siehe Sedlmeier S.223.
- 💡 C ist falsch: Der Student vermutet: Je niedriger die Temperatur, desto höher der Preis. Das ist eine ℹ️ negative Korrelation.
- 💡 D ist falsch: Der Student ist nicht der Merkmalsträger, sondern der Beobachter/Forscher/Autor der Studie... Der Merkmalsträger ist der Tag oder der jeweilige Zeitpunkt mit den beiden Merkmalen Temperatur und Benzinpreis.
- 💡 E ist richtig: Richtig ist auf jeden Fall, dass die Power bei einem einseitigen Test größer ist als bei einem zweiseitigen Test (siehe oben bei Aufgabe 4) und dass ein einseitiger Test somit eher signifikant würde. Und da die Fragestellung in der Aufgabe lautet: "Was könnten plausible Gründe für das Ergebnis sein?", sollte diese Aussage wohl in jedem Fall als richtig bewertet werden. Mehr hatte der Lehrstuhl dabei sicher nicht im Sinn. Aber tatsächlich kann man das sogar ausrechnen und es lässt sich (z.B.) ℹ️ mit R ganz konkret nachvollziehen.
Aufgabe 10
Welche Aussagen sind richtig?
Es geht um Konfidenzintervalle.
Lösungen:
- 💡 A ist richtig: Beim KI habe ich nicht einfach nur einen Schätzwert, der besagt: der wahre Wert ist hier irgendwo in der Nähe. Sondern ich präzisiere meine Aussage, indem ich sage, mit welcher "Verlässlichkeit/Genauigkeit" der wahre Wert in einem bestimmten Bereich ist.
- 💡 B ist falsch: Ein KI wird immer um den Kennwert eine Stichprobe herum gebildet. Zum Beispiel: Ein KI für µ wird um den Stichproben-Mittelwert Xquer herum gebildet. Xquer ist ein Schätzwert für µ. Und das KI ist ein Schätzintervall für µ.
- 💡 C ist richtig: Achtung! Das ist aus meiner Sicht eine fehlerhafte Klausurbewertung . So wie es da steht, ist die Aussage falsch!
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.ℹ️ Noch ein paar ergänzende Erläuterungen. - 💡 D ist falsch: Diese Aussage wird als falsch bewertet, weil die Null im Konfidenzintervall enthalten ist. Aber genau genommen, ist die Aufgabe etwas unpräzise. Denn es steht gar nicht dabei, wie die Nullhypothese ist. Die Aussage ist genau dann als eindeutig falsch zu bewerten, wenn die Nullhypothese besagt: die wahre Differenz in der Population ist null. Das ist zwar häufig so, aber eben nicht immer. Genau dieser Umstand wurde in anderen Klausuraufgaben schon explizit abgefragt. Da man die genaue Nullhypothese nicht kennt, lässt sich diese Aussage eigentlich gar nicht eindeutig bewerten...
- 💡 E ist richtig: Sofern ein t-Test für einen Mittelwert-Unterschied gemeint ist. ℹ️ Beispiel.


Hallo Guido,
Im Frage 9 E, ist von zweiseitigen Test die Rede. Aber die Vermutung ‚Je kälter…, desto teurer‘ spricht für eine gerichtete und somit für eine einseitige Test. Wäre die Frage damit nicht falsch zu bewerten?
Lg
Im Aufgabentext steht doch: Die Korrelation wird bei einem ZWEIseitigen Test nicht signifikant 🙂
Hallo Guido,
Bei Fragen 10E, hat EIN KI brim einseitigen Test keins Obergrenze weil es bis unendlich geht?
Vishakha
Entschuldigung, das Beispiel hat es erklärt. Es hat such erledigt. Danke.
Vishakha
Guido, herzlichen Dank! Ich finde es genial Antworten mit Erklärungen zu haben!!!