Lösungen 09 / 2021 – Teil 2

ℹ️ Hinweis  ← (hier klicken)

Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.
Aufgabe 10

Die Aufgabe ist ähnlich zu Aufgabe 7 aus der Klausur 03/2021.

In dieser Aufgabe geht es darum, wie man bei einem t-Test die Teststärke (Power) verändern kann.

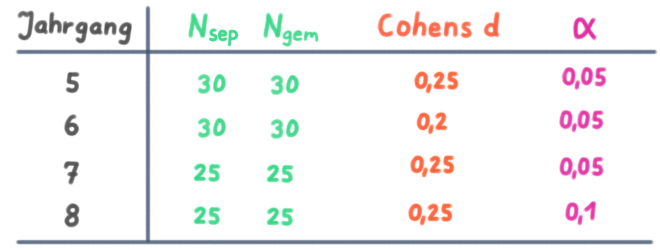
Es gibt eine Tabelle mit den Daten für vier verschiedene ℹ️ t-Tests für unabhängige Stichproben. Für jeden dieser t-Tests wurde ein separates Experiment durchgeführt. Es sind jeweils die folgenden Daten angegeben:

▪️ Die Größen ℹ️ der beiden unabhängigen Stichproben

▪️ Die Effektgröße Cohens d

▪️ Das Signifikanzniveau Alpha (α)

☝️Es sind genau diese drei Größen, die einen Einfluss auf die Teststärke (Power) haben.
☝️ Achtung, das Cohens d in der Tabelle steht nicht für den Unterschied der Gruppen in der Stichprobe, sondern für den in der H1 postulierten Effekt in der Population. Das ist in der Aufgabe ℹ️ fehlerhaft dargestellt.

In der Aufgabe geht es darum, in welcher Weise die Power jeweils beeinflusst wird.

Wir müssen also wissen, wie ist der Zusammenhang zwischen:

1) Cohens d und Power

2) Stichprobengröße und Power

3) Alpha (α) und Power

☝️Für alle drei Angaben gilt: Je größer der jeweilige Wert, desto größer die Power.

1) Je größer Cohens d desto größer die Power:

2) Je größer die Stichprobe desto größer die Power:

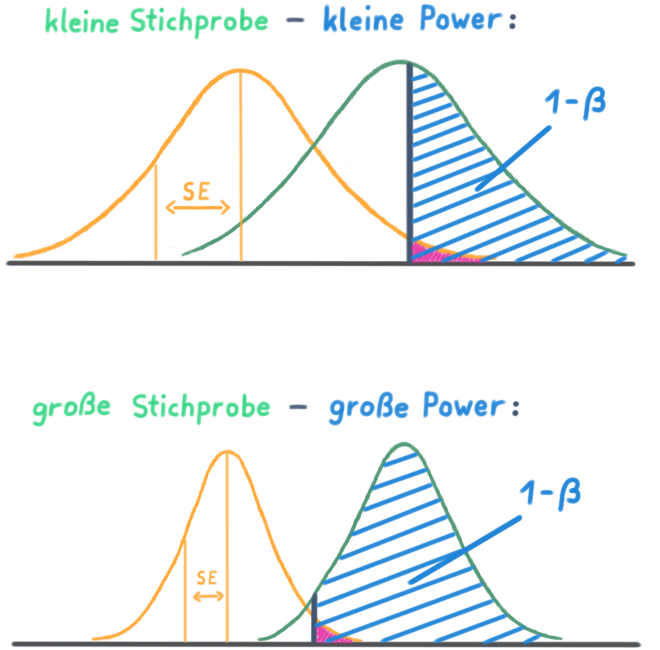
Je größer die Stichprobe, desto kleiner der Standardfehler (SE) und desto schmaler die Stichprobenverteilung.

Je größer die Stichprobe, desto genauer die Schätzung.

3) Je größer Alpha (α) desto größer die Power:

Je größer α, desto kleiner β.

Je größer α, desto größer 1-β.

Mit diesem Wissen sind die Aussagen in der Aufgabe leicht zu bewerten. Hier ist nochmal die Tabelle:

Lösungen:

  • 💡  A ist richtig:  In Jahrgang 5 sind die Stichproben größer.
  • 💡  B ist falsch:  In Jahrgang 8 ist Alpha (α) größer.
  • 💡  C ist falsch:  In Jahrgang 5 ist Cohens d größer.
  • 💡  D ist richtig:  ℹ️ Zwei Anmerkungen zu dieser Aussage… Warum also sollte man statt Cohens d den Korrelationskoeffizient r berechnen? ℹ️ Wieso ist eine solche Berechnung möglich und sinnvoll? Und: ℹ️ Warum sollte das überhaupt wichtig sein?
  • 💡  E ist richtig:  ℹ️ Power-Berechnung mit R für alle vier Beispiele.
Um diese Inhalte zu nutzen, musst du dich anmelden und den Zugriff auf die Klausurlösungen kostenpflichtig erwerben.

3 Gedanken zu „Lösungen 09 / 2021 – Teil 2“

    1. Aus dem Aufgabentext geht hervor, dass der p-Wert für den Test kleiner als 0,001 war. Welches Signifikanzniveau der Autor eigentlich im Sinn hatte, weiß man nicht, aber das ist auch egal. Denn kleiner als 0,001 bedeutet halt auch kleiner als 0,05. Und das bedeutet signifikant bei einem Niveau von 5%.

  2. Danke lieber Guido.

    Rückblickend und ohne die vermehrte Produktion von Stresshormonen, was bei mir gelegentlich zu kognitiven Blockaden führt ;)) in der Prüfungssituatin, war die Klausur doch recht einfach.

    Liebe grüße aus Berlin

Schreibe einen Kommentar